簡單而言，與傳統的回歸分析不同，結構方程分析能同時處理多個因變量，并可比較及評價不同的理論模型。與傳統的探索性因子分析不同，在結構方程模型中，可以通過提出一個特定的因子結構，并檢驗它是否吻合數據。通過結構方程多組分析，我們可以了解不同組別內各變量的關系是否保持不變，各因子的均值是否有***差異。樣本大小從理論上講：樣本容量越大越好。Boomsma（1982）建議，樣本容量**少大于100，比較好大于200以上。對于不同的模型，要求有所不一樣。一般要求如下：N/P〉10；N/t〉5；其中N為樣本容量，t為自由估計參數的數目，p為指標數目。很多情況下，可以把模型檢測和各種抽象與歸納原則結合起來驗證非有窮狀態系統(如實時系統)。黃浦區正規驗證模型優勢

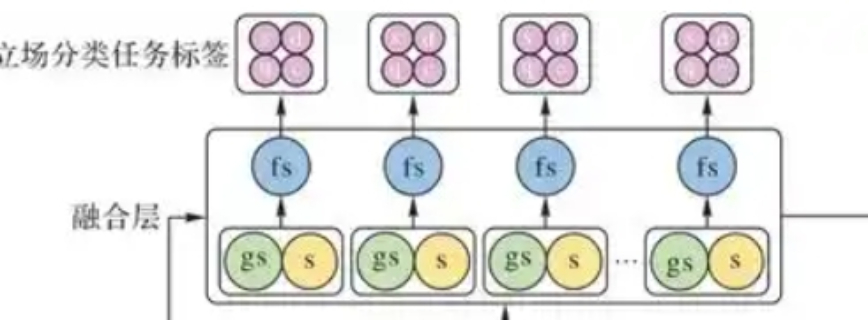
因為在實際的訓練中，訓練的結果對于訓練集的擬合程度通常還是挺好的（初始條件敏感），但是對于訓練集之外的數據的擬合程度通常就不那么令人滿意了。因此我們通常并不會把所有的數據集都拿來訓練，而是分出一部分來（這一部分不參加訓練）對訓練集生成的參數進行測試，相對客觀的判斷這些參數對訓練集之外的數據的符合程度。這種思想就稱為交叉驗證（Cross Validation） [1]。交叉驗證（Cross Validation），有的時候也稱作循環估計（Rotation Estimation），是一種統計學上將數據樣本切割成較小子集的實用方法，該理論是由Seymour Geisser提出的。長寧區自動驗證模型介紹K折交叉驗證：將數據集分為K個子集，模型在K-1個子集上訓練，并在剩下的一個子集上測試。

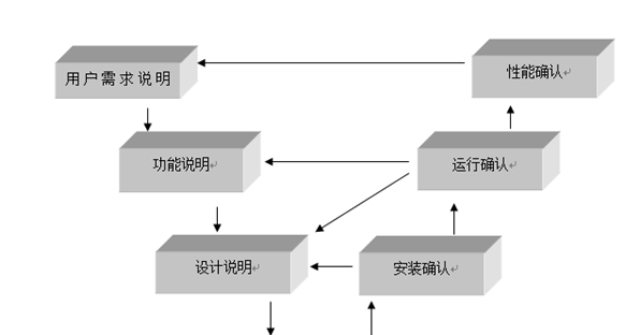
模型檢驗是確定模型的正確性、有效性和可信性的研究與測試過程。一般包括兩個方面：一是驗證所建模型即是建模者構想中的模型;二是驗證所建模型能夠反映真實系統的行為特征；有時特指前一種檢驗。可以分為四類情況：（1）模型結構適合性檢驗：量綱一致性、方程式極端條件檢驗、模型界限是否合適。（2）模型行為適合性檢驗：參數靈敏度、結構靈敏度。（3）模型結構與實際系統一致性檢驗:外觀檢驗、參數含義及其數值。（4）模型行為與實際系統一致性檢驗：模型行為是否能重現參考模式、模型的極端行為、極端條件下的模擬、統計學方法的檢驗。以上各類檢驗需要綜合加以運用。有觀點認為模型與實際系統的一致性是不可能被**終證實的，任何檢驗只能考察模型的有限方面。 [1]

極大似然估計法（ML）是結構方程分析**常用的方法，ML方法的前提條件是變量是多元正態分布的。數據的非正態性可以通過偏度（skew）和峰度（kurtosis）來表示。偏度表示數據的對稱性，峰度表示數據平坦性的。LISREL中包含的估計方法有：ML（極大似然）、GLS（廣義**小二乘法）、WLS（一般加權**小二乘法）等，WLS并不要求數據是正態的。 [2]極大似然估計法（ML）是結構方程分析**常用的方法，ML方法的前提條件是變量是多元正態分布的。數據的非正態性可以通過偏度（skew）和峰度（kurtosis）來表示。偏度表示數據的對稱性，峰度表示數據平坦性的。LISREL中包含的估計方法有：ML（極大似然）、GLS（廣義**小二乘法）、WLS（一般加權**小二乘法）等，WLS并不要求數據是正態的。 [2]常見的有K折交叉驗證，將數據集分為K個子集，輪流使用其中一個子集作為測試集，其余作為訓練集。

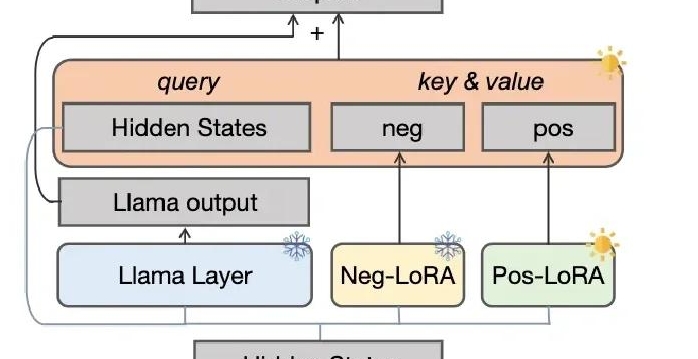
在產生模型分析（即 MG 類模型）中，模型應用者先提出一個或多個基本模型，然后檢查這些模型是否擬合樣本數據，基于理論或樣本數據，分析找出模型擬合不好的部分，據此修改模型，并通過同一的樣本數據或同類的其他樣本數據，去檢查修正模型的擬合程度。這樣一個整個的分析過程的目的就是要產生一個比較好的模型。因此，結構方程除可用作驗證模型和比較不同的模型外，也可以用作評估模型及修正模型。一些結構方程模型的應用人員都是先從一個預設的模型開始，然后將此模型與所掌握的樣本數據相互印證。如果發現預設的模型與樣本數據擬合的并不是很好，那么就將預設的模型進行修改，然后再檢驗，不斷重復這么一個過程，直至**終獲得一個模型應用人員認為與數據擬合度達到他的滿意度，而同時各個參數估計值也有合理解釋的模型。 [3]將驗證和優化后的模型部署到實際應用中。奉賢區銷售驗證模型訂制價格

將數據集分為訓練集和測試集，通常按70%/30%或80%/20%的比例劃分。黃浦區正規驗證模型優勢

在進行模型校準時要依次確定用于校準的參數和關鍵圖案，并建立校準過程的評估標準。校準參數和校準圖案的選擇結果直接影響校準后光刻膠模型的準確性和校準的運行時間，如圖4所示 [4]。準參數包括曝光、烘烤、顯影等工藝參數和光酸擴散長度等光刻膠物理化學參數，如圖5所示 [5]。關鍵圖案的選擇方式主要包含基于經驗的選擇方式、隨機選擇方式、根據圖案密度等特性選擇的方式、主成分分析選擇方式、高維空間映射的選擇方式、基于復雜數學模型的自動選擇方式、頻譜聚類選擇方式、基于頻譜覆蓋率的選擇方式等 [2]。校準過程的評估標準通常使用模型預測值與晶圓測量值之間的偏差的均方根（RMS）。黃浦區正規驗證模型優勢

上海優服優科模型科技有限公司是一家有著雄厚實力背景、信譽可靠、勵精圖治、展望未來、有夢想有目標，有組織有體系的公司，堅持于帶領員工在未來的道路上大放光明，攜手共畫藍圖，在上海市等地區的商務服務行業中積累了大批忠誠的客戶粉絲源，也收獲了良好的用戶口碑，為公司的發展奠定的良好的行業基礎，也希望未來公司能成為*****，努力為行業領域的發展奉獻出自己的一份力量，我們相信精益求精的工作態度和不斷的完善創新理念以及自強不息，斗志昂揚的的企業精神將**上海優服優科模型科技供應和您一起攜手步入輝煌，共創佳績，一直以來，公司貫徹執行科學管理、創新發展、誠實守信的方針，員工精誠努力，協同奮取，以品質、服務來贏得市場，我們一直在路上！